looking back at all the literature that was published on the topic of deep learning in 2014 is quite overwhelming. at times it has felt that nearly every week a new paper from some heavyweights was being circulated via arxiv. trying to do a review of all that work would be a fool’s errand, but i thought it might be worthwhile to summarize some of the threads that i found particularly interesting. below i group papers by broader topic.

exploring different architectures

while deep nets promise to free you from designing low and mid level features by hand, designing the architecture for a network is still somewhat of a black art (which is still quickly evolving). a number of papers this year explored alternatives to the popular “alex-net” architecture:

network in network, lin et al.

[paper link]

a typical convolutional net consists of convolutional layers (i.e. a number of small filters is applied to the input), following by a non-linearity (e.g. sigmoid, rectified linear unit, etc), followed by max pooling (this is repeated a few times, and typically topped off with a couple fully connected layers). the authors of “network in network” argue that the linear filtering operation in the convo layers is not expressive enough, leading to a necessity of many layers stacked on top of each other. they propose that instead of a linear filter, one can use a small multi-layered perceptron that slides over the input channels. the following diagram illustrates such a layer:

NIN

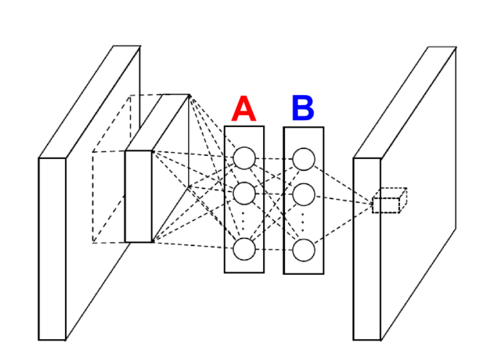
here we see a two-layer network, with layers A and B, being slid over the input channels. now, the interesting thing the authors point out is that this is equivalent to a regular convolutional layer, followed by one or more 1x1 convolutional layers. this took me some time to grok, but it’s worth understanding since this building block comes up again in the googlenet architecture and has some interesting consequences. here’s how i think about it: in the figure above, the neurons in the A box are actually the same as a regular convolutional layer – each one corresponds to a linear filter + non-linearity. i.e., if there are 16 neurons in the A box, this is the same as a convolutional layer with 16 filters/output channels. each neuron in the B box takes a linear combination of the outputs of neurons in A, and pass those through a non-linearity. this is precisely what a 1x1 convolutional layer would do, so layer B is akin to having a bunch of 1x1 convolutional layers and stacking their outputs together. if there are more layers in the “inner network”, they would be akin to doing this 1x1 convolutional layer operation again on the output of B.

deeply supervised nets, lee et al.

[paper link]

the typical architecture for a convolutional net will have a softmax layer at the top followed by the cross entropy loss function. the error is then propagated from the top down to the inner layers in the network. the main idea in “deeply supervised nets” is to tie some of the inner layers more directly to the objective function. it’s not entirely clear to me why this would help versus hinder the learning process, but it’s certainly an idea worth investigating (and an easy trick to try) considering the fact that vanishing gradients is a common problem faced by neural net practitioners.

(googlenet) going deeper with convolutions, szegedy et al.

[paper link]

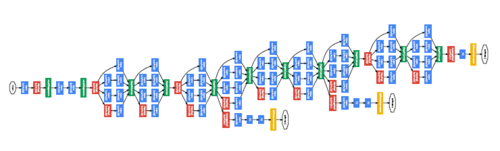
googlenet

the googlenet team did very well in the imagenet competition this year (http://www.image-net.org/challenges/LSVRC/2014/results). the architecture described in the paper looks totally insane. even though the authors break things down and explain some of the intuition, a lot of architecture decisions seem somewhat arbitrary to me and the final the results is almost a parody of itself. that said, i did want to highlight a few of the ideas/arguments in the paper that i thought were interesting:

  1. the deeper the better (this is, of course, a recurring theme in the last couple of years)

  2. a really deep architecture will inevitably lead to a crazy number of parameters that need to trained. the get around this, the googlenet architecture borrows the 1x1 conv layer trick from “network in network”. the idea is that you can reduce the number of channels this way – suppose at some point in your network you have 256 channels, if you follow this with a convolutional layer with 32 1x1 filters, you effectively perform dimensionality reduction from 256 channels to 32, thereby reducing the number of parameters (since layers down the line now need to deal with fewer inputs).

  3. as with the “deeply supervised nets” paper above, multiple layers in the googlenet architecture are tied to the objective function, though these two pieces of work came out independently, and the authors of googlenet have more of a “multi-scale invariance” argument for doing this (versus regularization).

(vgg) very deep convolutional networks for large-scale image recognition, simonyan & zisserman

[paper link]

the architecture developed by the team at oxford performs more or less as well as googlenet, and while the central concept is again “deeper is better”, the overall design is much much more elegant. this architecture is essentially the same as the trusty alex-net, except it replaces convolutional layers with wide filters (e.g. 7x7), with stacks of convolutional layers with smaller (3x3) filters (with no max pooling in between). the argument for this is as follows. a single 7x7 conv layer has a total of 49 parameters, whereas a stack of 3 3x3 layers has 27. at the same time, 3 convolutions with 3x3 filters is equivalent to a single convolution with a 7x7 filter (this isn’t entirely true because of the non-linearities in between the 3x3 convolutional layers, but close enough for intuition purposes), so you can think of this as replacing the 7x7 layer with something equivalent but more regularized (since not all 7x7 filters can be decomposed into 3 3x3 filters).

aside from this, there a bunch more details in the paper about how to deal with scale and cropping during training and runtime that i will omit here.

all in all, if i had to pick an architecture for a visual recognition problem today, i would probably pick this one. it works well and is simpler to understand than the rest.

model compression

if you peruse any kaggle or imagenet competition you will notice that almost all the winning entries are ensembles of classifiers. training several classifiers (with different initialization, different subsets of the dataset, etc) and combining them via simple voting is a safe and proven way to obtain a couple extra percentage points of accuracy. however, using such models in practice comes at an obvious computational cost.

as mentioned above, another common theme of many recent deep net papers has been that deeper models tend to outperform shallower models (despite the fact that, theoretically speaking, a shallow model can have as much representational power as one could want, as long as you increase the number of hidden units). as with ensembles, deeper models also come at a cost – the more layers & connections, the more computation you have to do to make a prediction (and even if you keep the number of parameters the same, a deeper model is more difficult to parallelize than a shallow model).

caruara et al and hinton et al have published some very interesting results this year about the concept of model compression (the concept was originally covered in caruana’s 2006 paper, but has made a come back this year). that is, if you have an ensemble of beefy nets, you could train a single shallow(er) net that achieves almost the same level of accuracy. the “one weird trick” to achieve this is as follows: first, train your beefy nets as usual; then take a (preferably held out) dataset, and run it through the beefy model, and save the output of the penultimate layer (right before the softmax); finally, train a smaller/shallower net to predict those outputs rather than the ground truth labels.

this is indeed a fascinating result. it highlights the fact that deep models are not necessarily more expressive than smaller/shallower nets, but rather that we just haven’t found a good enough optimization procedure to train shallow nets — though now we appear to have a hack around it.

this result is also quite important in practice. i imagine many practitioners will use trick to obtain faster results at runtime and reduce the memory footprint of their models.

fine tuning

there have been a lot of papers recently showing how one can take a network trained on a large dataset like imagenet and adapt it to other tasks by using the trained net as initialization and continuing to train on the new data (i.e. “fine-tuning”). however, i haven’t seen a thorough empirical study of fine tuning until yosinski et al. the authors explore how performance varies depending on how many layers you pre-train on another dataset, and which layers you fine tune afterwards (either only the new ones or all of them). there are a lot of interesting bits in the paper so i really recommend going through it, but the TLDR is: when in doubt, fine tune all the layers. i’d be curious to find out how exactly they set the learning rates when fine tuning a combination of pre-trained and new layers (e.g. it might make sense to set the learning rate for the new layers to be much higher) – i wasn’t able to find this in the paper. this issue is, however, discussed in branson et al. where they propose an interesting trick: first lock the pre-trained layers and fine-tune only the new layers (until they get to some reasonable state), then unlock the pre-trained layers and fine-tune all of them together.

recurrent nets

sequence to sequence learning with neural networks, sutskever et al.

i’ve only recently started reading up on recurrent nets, so i don’t have as deep of a context here, but this paper looked really intriguing. to quote someone’s account of nips 2014, ilya sutskever (first author of this paper), “declared that all supervised vector-to-vector problems are now solved thanks to deep feed-forward neural networks, and then proceeded to declare that all supervised sequence-to-sequence problems are now solved thanks to deep LSTM networks”.

the high level goal of the paper is to train a network that is able to take a sequence (of vectors) of variable length and map it into another sequence of a possibly different length (the obvious application being machine translation). to do this, the authors propose a siamese sort of architecture where one piece maps the input sequence into a single point in some high dimensional space, and the other “unwraps” this point into an output sequence. the mapping and unwrapping is done via LSTMs. the “one weird trick” of this paper is that the input sequence is fed into the network in reverse order. this is done so that the first element of the output sequence will be right next to the first element of the input sequence. the intuition is that this makes learning easier since the two corresponding pieces of the two sequences are close to each other; if one were to arrange the input and output sequences in their normal orientation, gradients between corresponding pieces would have to travel some arbitrary distance (~ the length of the input sequence) and even with LSTM this becomes tough. apparently this trick is pretty pivotal in getting good performance.

so there you have it. i’ve obviously left many things out (the string of image captioning papers, techniques for distributed training, etc), but the above are the topics that i thought would be of interest to most practitioners. what were your favorite deep net (or machine learning in general) papers in 2014?